Elbow angle
| Type | Python Script |
|---|---|
| Download | elbow_angle.py |
| Author(s) | Jared Sampson |
| License | BSD |
| This code has been put under version control in the project Pymol-script-repo | |
Introduction
This script allows you to calculate the elbow angle of an antibody Fab fragment object and optionally draw a graphical representation of the vectors used to calculate the elbow angle.
Syntax
elbow_angle object [, light=L [, heavy=H [, limit_l=107 [, limit_h=113 [, draw=0 ]]]]]
The first argument should be a PyMOL object. You can calculate the elbow angles of multiple Fabs from the same object (one at a time) by specifying the chains manually for each Fab.
The `light` and `heavy` arguments are for PDB chain IDs, and `limit_l` and `limit_h` are the last residue of the light and heavy chain variable domains, respectively. (For Kabat-numbered structures, these limits will be 107 and 113, respectively. For structures with different numbering schemes, the limits can be estimated by visual inspection of the PDB file.) Setting `draw=1` will draw the "dumbbells" seen in the images below.
Examples
Basic usage
# load an antibody Fab fragment from the PDB
fetch 3ghe, async=0
# calculate the elbow angle and draw the vectors
elbow_angle 3ghe, draw=1
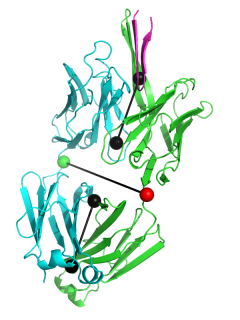
This will produce something like the first image below.
Note that if you don't specify the light/heavy chain IDs or the variable domain limit residue numbers, the default values (L/H and 107/113, respectively) will be used. If your antibody is not Kabat or Chothia numbered, or has different chain names, this will result in an incorrect value or, in the case of wrong chain IDs, may cause the script to fail entirely due to an empty selection. Have a look at Dr. Andrew Martin's Abnum for more information on antibody numbering.
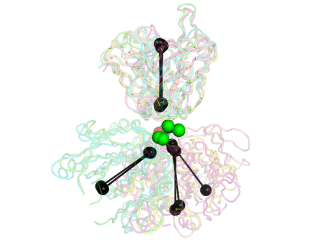
The black "dumbbells" pass through the centers of mass of the variable and constant domains of each Fab (as determined using com.py). The green and red dumbbells denote the residues used to split the variable and constant domains, with a green ball for the light chain, and a red ball for the heavy chain.
Included Example
There is also an example .pml file in the Pymol-script-repo/examples directory which can be run by the following:
import ex
ex elbow_angle
This will run the following .pml file:
| Type | PyMOL Script |
|---|---|
| Download | examples/elbow_angle.pml |
| Author(s) | Jared Sampson |
| License | BSD |
| This code has been put under version control in the project Pymol-script-repo | |
reinitialize
import elbow_angle
bg_color white
# example structures from Stanfield, et al. JMB 2006
# doi:10.1016/j.jmb.2006.01.023
fetch 1bbd, async=0
fetch 7fab, async=0
fetch 1dba, async=0
fetch 1plg, async=0
fetch 1nl0, async=0
dss
as cartoon
set cartoon_transparency, 0.7
remove all and not chain L+H
util.mass_align("1bbd and ((chain L and resi 1-114) or (chain H and resi 1-118))")
# adopt a similar view to Figure 1 in Stanfield, et al.
set_view (\
-0.953261435, -0.226005003, 0.200535893,\
-0.230026290, 0.112494141, -0.966659248,\
0.195909262, -0.967606425, -0.159222543,\
0.000000000, 0.000000000, -230.122619629,\
62.279075623, 48.879341125, 138.177505493,\
181.430419922, 278.814819336, -20.000000000 )
# 1bbd
# Stanfield: 127 deg
# elbow_angle.py: 125 deg
elbow_angle 1bbd, limit_l=114, limit_h=118, draw=1
# 7fab
# Stanfield: 132 deg
# elbow_angle.py: 126 deg
elbow_angle 7fab, limit_l=104, limit_h=117, draw=1
# 1dba
# Stanfield: 183 deg
# elbow_angle.py: 176 deg
elbow_angle 1dba, draw=1
# 1plg
# Stanfield: 190 deg
# elbow_angle.py: 189 deg
elbow_angle 1plg, limit_l=112, limit_h=117, draw=1
# 1nl0
# Stanfield: 220 deg
# elbow_angle.py: 221 deg
elbow_angle 1nl0, draw=1
and will produce the second image above.
Implementation
The elbow angle is the angle between the pseudo-twofold axes between the light and heavy chain variable and constant domains, respectively. The rotation matrix to superpose VL onto VH and CL onto CH are calculated and the vectors corresponding to the rotation axes are determined (using Christoph Gohlke's transformations.py). The elbow angle is the obtuse angle obtained by taking the arccos of the dot product of the two vectors. For consistency, the elbow angle is reported as less than 180° when the cross product of the Variable and Constant domain rotation axis vectors ( V ⨯ C ) is a vector pointing the same direction as that from the limit_h residue alpha carbon atom to the limit_l alpha carbon atom.